definisi lingkaran
lingkaran adalah himpunan semua titik pada bidang dalam jarak tertentu, yang disebut jari-jari, dari suatu titik tertentu, yang disebut pusat. Lingkaran adalah contoh dari kurva tertutup sederhana, membagi bidang menjadi bagian dalam dan bagian luar.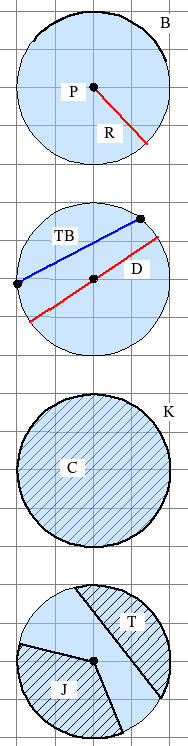
- Titik pusat (P)
- merupakan titik tengah lingkaran, dimana jarak titik tersebut dengan titik manapun pada lingkaran selalu tetap.
- Jari-jari (R)
merupakan garis lurus yang menghubungkan titik pusat dengan lingkaran. - Tali busur (TB)
merupakan garis lurus di dalam lingkaran yang memotong lingkaran pada dua titik yang berbeda. - Busur (B)
merupakan garis lengkung baik terbuka, maupun tertutup yang berimpit dengan lingkaran. - Keliling lingkaran (K)
merupakan busur terpanjang pada lingkaran. - Diameter (D)
merupakan tali busur terbesar yang panjangnya adalah dua kali dari jari-jarinya. Diameter ini membagi lingkaran sama luas. - Apotema
merupakan garis terpendek antara tali busur dan pusat lingkaran. - Juring (J)
merupakan daerah pada lingkaran yang dibatasi oleh busur dan dua buah jari-jari yang berada pada kedua ujungnya. - Tembereng (T)
merupakan daerah pada lingkaran yang dibatasi oleh sebuah busur dengan tali busurnya. - Cakram (C)
merupakan semua daerah yang berada di dalam lingkaran. Luasnya yaitu jari-jari kuadrat dikalikan dengan pi. Cakram merupakan juring terbesar.
persamaan lingkaran
Suatu lingkaran memiliki persamaan
 adalah jari-jari lingkaran dan
adalah jari-jari lingkaran dan 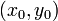 adalah koordinat pusat lingkaran.
adalah koordinat pusat lingkaran.Jika pusat lingkaran terdapat di
 , maka persamaan di atas dapat dituliskan sebagai
, maka persamaan di atas dapat dituliskan sebagai adalah jari-jari lingkaran dan
adalah jari-jari lingkaran dan 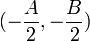 adalah koordinat pusat lingkaran. Bentuk persamaan tersebut dikenal sebagai bentuk umum persamaan lingkaran.
adalah koordinat pusat lingkaran. Bentuk persamaan tersebut dikenal sebagai bentuk umum persamaan lingkaran.Persamaan parametrik
Lingkaran dapat pula dirumuskan dalam suatu persamaan parameterik, yaituLuas lingkaran
Luas lingkaran
 dan jari-jari luar
dan jari-jari luar 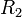 .
.Penjumlahan elemen juring

Luas lingkaran dapat dihitung dengan memotong-motongnya sebagai elemen-elemen dari suatu juring untuk kemudian disusun ulang menjadi sebuah persegi panjang yang luasnya dapat dengan mudah dihitung. Dalam gambar r berarti sama dengan R yaitu jari-jari lingkaran.
Luas juring
Luas juring suatu lingkaran dapat dihitung apabila luas lingkaran dijadikan fungsi dari R dan θ, yaitu;Luas cincin lingkaran
Suatu cincin lingkaran memiliki luas yang bergantung pada jari-jari dalam dan jari-jari luar
dan jari-jari luar 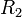 , yaitu
, yaitu rumus ini kembali menjadi rumus luas lingkaran.
rumus ini kembali menjadi rumus luas lingkaran.Luas potongan cincin lingkaran
Dengan menggabungkan kedua rumus sebelumnya, dapat diperolehKeliling lingkaran
Keliling lingkaran memiliki rumus:Panjang busur lingkaran
Panjang busur suatu lingkaran dapat dihitung dengan menggunakan rumus mengisyaratkan bahwa terdapat dua buah kurva, yaitu bagian atas dan
bagian bawah. Keduanya identik (ingat definisi lingkaran), sehingga
sebenarnya hanya perlu dihitung sekali dan hasilnya dikalikan dua.
mengisyaratkan bahwa terdapat dua buah kurva, yaitu bagian atas dan
bagian bawah. Keduanya identik (ingat definisi lingkaran), sehingga
sebenarnya hanya perlu dihitung sekali dan hasilnya dikalikan dua.
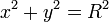
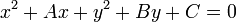



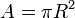



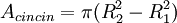
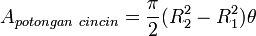
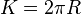
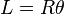
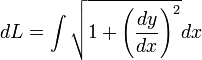
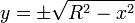

materinya bagus va,,, tetapi kayaknya kalau disertai contoh soal akan lebih membantu untuk menerapkan rumusnya,, :)
BalasHapusya makasih,, nanti vha perbaikki, dan soalnya vha masukkin :)
BalasHapusmaterinya bagus, cukup jelas dan mudah dipahami,,,,,,,tp akan lebih bagus lagi jika disertai dgn contoh-contoh soalnya,,,,,,,,,,,,,,mksh eva
BalasHapusTampilan blog nya bagus.
BalasHapusjuga materinya bagus, inga Eva... tapi boleh ditambah dengan contoh soal.
fighting ^_^
ok.. makasih semua :)
BalasHapusMaterinya bgus dan mnarik :)
BalasHapusMaterinya bgus dan mnarik :)
BalasHapusMaterinya bgus dan mnarik :)
BalasHapusmakasih sobat @cece
BalasHapusmaterinya bagus tpi c0bah dikasih c0nt0h agar Iebih jeIas va
BalasHapusbagus2 materinya tapi tambahkan contohnya dong kwan.
BalasHapusmaterinya bagus.. tambahan saja untuk masukkan cntoh biar lebih lengkap...
BalasHapus